Shortest Circular Paths
The shortest circular path problem is a generalization of the standard shortest path problem. While the standard shortest path problem aims at finding a shortest path between two known nodes in a graph, the shortest circular path problem is to find a closed path with minimum cost. This problem is more difficult than the standard shortest path problem, since no explicit start or end node is known.
The most frequently used brute-force approach to shortest circular paths has a complexity of O(n^3). Our algorithm reduces the worst-case complexity to only O(n^2 log n), while being close to O(n^2) in practice.
Applications of shortest circular paths are in contour-based object segmentation, shape matching, DNA sequence comparison, or cyclic code decoders.
Algorithm
Version 1, see ICCV paper. Version 2 will be disclosed after publication.
Example Results
Shown are the computation times in seconds for worst-case inputs (noise). The brute-force dynamic programming approach with O(n^3) is not shown, since it is much slower.
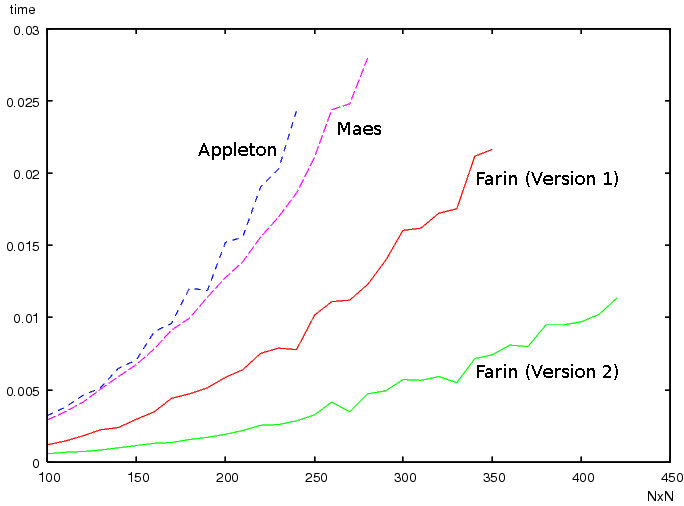
For comparison: Appleton is about O(n^2.6), Maes is O(n^2 log n).
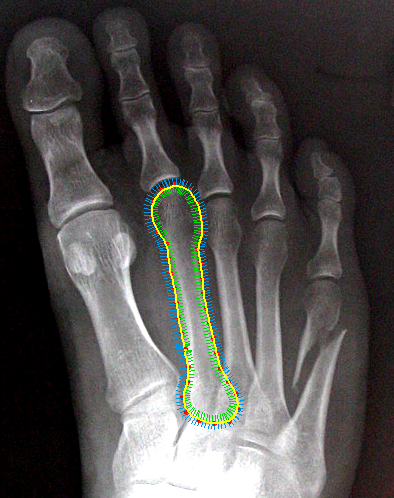
Application Example: Segmentation
For segmentation, we built a convenient user interface, in which the user coarsely marks the object of interest with a broad corridor. The image content in the corridor is flattened to achieve approximately the effect of obtaining a length-normalized shortest path solution.

The flattened corridor-graph that resulted from marking one of the cells looks as follows:

The shortest circular path is computed in horizontal direction and the obtained path is mapped back to the input image coordinates to give the object contour in the input image.
A more complex example:
Application Example: 2D Shape Matching
For shape-matching, correspondences between points on two contours have to be identified. Parameterizing the contours with i and j, respectively, gives a 2D grid graph with nodes v_{i;j}, where each node is attributed with a cost, obtained from local shape characteristics. Finding a minimum-cost circular path in this graph gives corresponding points on the two contours.
An example path found is shown below. Note that the edges connect the nodes in a torus topology. In the picture below, the actual graph has been duplicated and the red-lines identify corresponding, connected nodes.
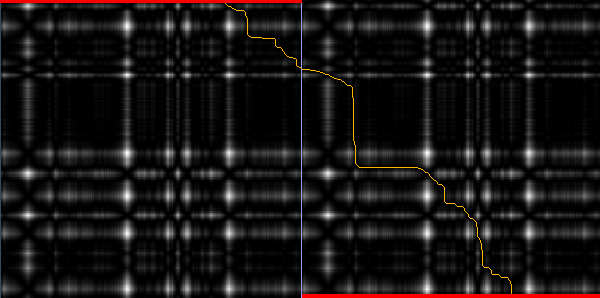
References
- Dirk Farin, Peter H. N. de With: "Shortest Circular Paths on Planar Graphs" in 27th Symposium on Information Theory in the Benelux, vol. p. 117-124, June 2006, Noordwijk, Netherlands.
- Dirk Farin, Magnus Pfeffer, Peter H. N. de With, Wolfgang Effelsberg: "Corrisor Scissors: A Semi-Automatic Segmentation Tool Employing Minimum-Cost Circular Paths" in International Conference on Image Processing (ICIP), vol. p. 1177-1180, Oct 2004, Singapore.
- Frank Schmidt, Dirk Farin, Daniel Cremers: "Fast Matching of Planar Shapes in Sub-cubic Runtime", accepted for ICCV 2007.