Multi-Sprite Background Generation for MPEG-4 Video Coding

Object-oriented coding in the MPEG-4 standard enables the separate processing of foreground objects and the scene background sprite. Since the background sprite only has to be sent once, transmission bandwidth can be saved. We have found that the counter-intuitive approach of splitting the background into several independent parts can reduce the overall amount of data.

In the general case, the synthesis of a single background sprite is even impossible and the scene background must be sent as multiple sprites instead. For this reason, we developed an algorithm that provides an optimal partitioning of a video sequence into independent background sprites (a multi-sprite), resulting in a significant reduction of the involved coding cost.

Additionally, our sprite-generation algorithm ensures that the sprite resolution is kept high enough to preserve all details of the input sequence, which is a problem especially during camera zoom-in operations. Even though our sprite generation algorithm creates multiple sprites instead of only a single background sprite, it is fully compatible with the existing MPEG-4 standard. The total coding cost for the sprite-VOP is reduced by a factor of about 2.6 or even higher, depending on the sequence.

The Problem

MPEG-4 sprite coding is based on the projective motion model, which in geometric terms is a plane-to-plane mapping (a homography). Thus, the sprite image can be envisioned as the collective projection of all input images onto a single image plane. This leads to increasing perspective image distortions, the more the camera rotates away from the frontal viewing angle. For a standard sprite, a rotating camera setup looks like this:

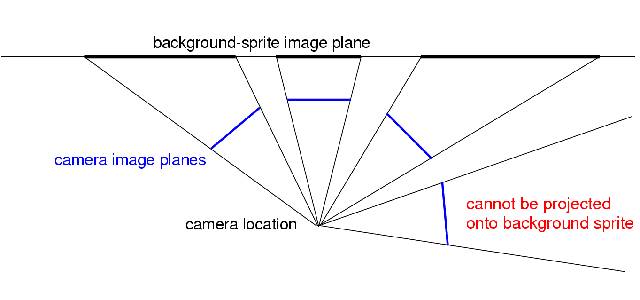
The Solution

Our solution to this problem is to use multiple image planes instead of only a single plane for the sprite. This leads to a set of sprite images, which we denote as multi-sprite. A multi-sprite can be constructed in such a way that image distortions are minimized and arbitrary camera movement can be processed. With multi-sprites, the same camera setup from above can now be handled like this:

In order to generate the multi-sprite, it must be decided how the input sequence should be divided into n ranges (1,p₁-1), (p₁,p₂-1), ..., (p_n-1,N). To this end, we compute the sprite-size ||S_a;b|| that would result from synthesizing a sprite for each range (a,b). Using this formulation, the partitioning problem can be formulated as finding the partitioning P={ (a_i,b_i) } which minimizes the total sum of sprite sizes.

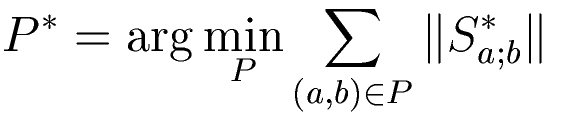
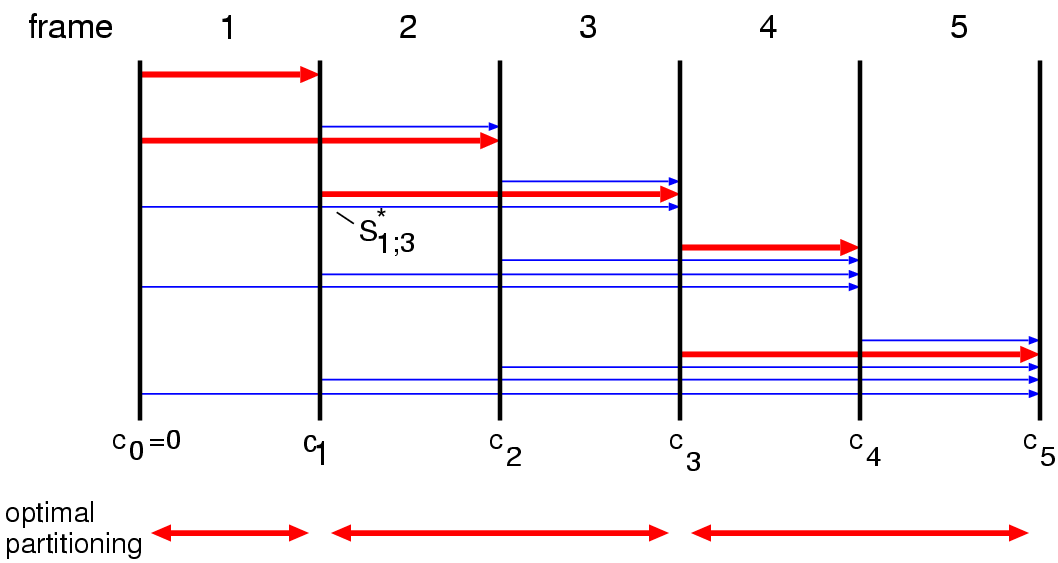
This can be solved very efficiently using dynamic programming, by iteratively computing the costs c_i, denoting the above sum upto frame i. Obvisouly, we start with c₀=0.

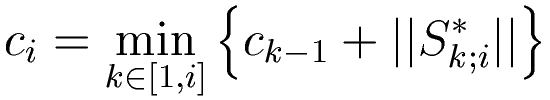
Backtracking the choices that were made during the computations of each c_i, we obtain the optimal partitioning.

Additionally, we can impose further constraints in the computation like a maximum sprite-buffer size, or a resolution-preservation constraint, without increasing the computational complexity. For details, see the papers below.

Examples and Test Data

Stefan sequence

We preprocessed the stefan-sequence by cropping away the black borders, which can introduce artifacts in the generated sprite. The sequence we used has size 346x280 and can be downloaded in raw yuv format (see below). First, a feature-based motion-estimator was applied to obtain the frame-to-frame motion parameters [2]. We provide these parameters in the download section below for your convenience in carrying out comparative studies (the parameters are the 3x3 homography matrices, in row-first order). Note that these are low-accuracy motion-parameters that are not used for sprite construction. For the actual sprite-construction (after multi-sprite partitioning), we refine the motion parameters with a dense matching approach. You can also find the high-accuracy parameters below. These high-accuracy parameters are not inter-image parameters, but relative to the sprite plane. If you use any of these parameters in your research, don't forget to cite the corresponding paper from below.

The following pictures are the obtained multi-sprite images (computed with an additional resolution preservation constraint, see [1]). The reference frame is marked in each picture. Select "View Image" to see the picture in full size.

The sprite partitioning data:

0-240 ref: 10 scale: 0.751164 bounding box size: 1020.97x378.076=386004
241-255 ref: 253 scale: 0.660012 bounding box size: 706.93x300.2=212220
256-291 ref: 268 scale: 0.652562 bounding box size: 795.731x313.339=249333
292-299 ref: 299 scale: 1 bounding box size: 420.828x339.888=143035

computation time: 0.964s (including computing full transitive closure and cost matrix)

Dataset

Physical camera parameters

By applying autocalibration techniques [3], the physical camera parameters (rotation angles, focal lengths) can be recovered from the motion data. This enables to get an overview about how the capturing took place.

Rail sequence

This sequence shows a more complicated camera motion. For your convenience, we again provide the sequence and motion parameters:

Sprite partitioning data:

0-44 ref: 32 scale: 0.796521 bounding box size: 541.444x445.22=241062
45-81 ref: 64 scale: 0.768932 bounding box size: 478.703x445.935=213471
82-139 ref: 97 scale: 0.775388 bounding box size: 455.324x386.728=176087

computation time: 0.224s

References

Dirk Farin, Peter H. N. de With: "Enabling Arbitrary Rotational Camera Motion Using Multisprites With Minimum Coding Cost" in IEEE Transactions on Circuits and Systems for Video Technology, April 2006
Dirk Farin, Peter H. N. de With: "Evaluation of a Feature-Based Global-Motion Estimation System" in Visual Communications and Image Processing, vol. 5960 p. 1331-1342, July 2005
Dirk Farin, Peter H. N. de With: "Estimating Physical Camera Parameters based on Multi-Sprite Motion Estimation" in SPIE Image and Video Communications and Processing, vol. 5685 p. 489-500, January 2005